Data - Information - Knowledge
In its basic form, data are various symbols and signs whose meaning becomes clear only when they are placed in context. Data is created by collecting and measuring observations and conditions. In most cases, data is sent, received and processed by machines. The data becomes information by linking it with additional content. Information represents knowledge about facts or persons. Knowledge arises from this and thus describes the collected information that is available about a particular state of affairs or a person. Knowledge about these facts makes it possible to make well-founded decisions and solve problems.
Data transmission modes in agriculture
A basic system of data exchange is characterized by the term IOT Internet of things. It describes an intelligent networking of devices, machines, fields and livestock. Through the transmitted information in real time, unnecessary routes, costs and time are to be saved. A key point here is the early detection of problems or even diseases. The Internet of Things is an intelligent network of sensors and processors that are connected to each other and the outside world via the Internet. In the process, the area-wide network relies on Internet access. There are different networks for this, such as LoRa, which collect data locally and transfer it to the server via a central point on the Internet.
LoRaWAN

Lora Alliance Logo
LoRaWAN stands for Long Range Wide Area Network and is a Low Power Wide Area Network (LPWAN or low energy wide area network) specification for wireless battery-powered systems in a regional, national or even global network and enables energy-efficient transmission of data over longer distances.
A LoRaWAN consists of at least three components: a sensor, a gateway and a LoRa server. The gateway forms the interface between the energy-efficient LoRa radio transmission and the powerful connection to the server. The sensor uses LoRa to send its data to all gateways in its vicinity. These gateways receive the data and forward it to the server. From this point on, the data can be individually processed, visualized and/or stored.
"LoRa" describes the radio technology and "LoRaWAN" describes the communication between each other and thus means the network.
However, there are other Low Power Wide Area Networks (LPWANs) in parallel with LoRaWAN. These include Sigfox and Nb-IoT (narrow band). The biggest difference between these technologies is the network structure.
Deployments e.g. in field sensors for the transmission of ground and weather data also at the LZSG.
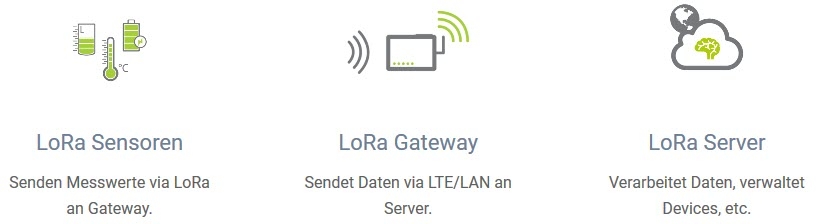
© linemetrics.com
Mobile data network

The mobile Internet is closely linked to advances in mobile communications technology. The start of data transmission via the mobile network marks the launch of the 2nd generation
GSM: Global System for Mobile Communications is a mobile communications standard introduced in 1990 for fully digital mobile networks, used mainly for telephony and short messages (SMS). Extensions to the standard such as GPRS and EDGE led to faster data transmission and heralded the following generations.
2nd generation (2G)
GPRS: General Packet Radio Service: A packet-oriented transmission service.
EDGE Enhanced Data Rates for GSM Evolution: Technique for increasing the data rate.
3rd generation (3G)
- UMTS: Universal Mobile Telecommunications System (UMTS) with the High Speed Packet Access (HSPA) extension with increased download and upload rates.
- LTE: Long Term Evolution Unlike UMTS, LTE supports different bandwidths and can therefore be used flexibly in different spectrums.
4th generation (4G/LTE)
- LTE-Advanced: LTE-Advanced is an extension of LTE that theoretically enables data rates of up to 3 Gbps.
5th generation (5G)
The 5th generation of mobile communications is expected to achieve data rates of up to 10 gigabits per second. That would be around 10 times as fast as the current LTE standard. 5G makes much more intensive use of all the resources that can be used for radio transmission. 5G is essentially based on three factors:
- intensive use of additional frequency bands (more than a billion frequencies can be used for 5G, which will be expanded in the coming years)
- dense network of antennas (indoor and outdoor) (the more the higher frequencies are used, the more losses occur in radio transmission and thus the range is shorter i.e. smartphones have to be closer to the antennas)
- very high number of end devices ( increasing communication lines between machine to machine (M2M) like e.g. for autonomous driving
CAN-BUS
Bus is the abbreviation for the "Binary Unit System". This system is used within a network for the transmission of data between the individual participants. The bus system is defined as the totality of all connections for sending and receiving data between the individual components and devices (functional units). It is practically a complex system of electronic miniature line paths. In principle, all functional units connected to a bus system can send and receive information. In order to prevent different devices/components from sending data at the same time and to ensure that only the devices/components for which the currently sent data is intended are ready to receive, bus systems must be managed very precisely. Usually this is done by the processor, often also by a dedicated bus controller.
The CAN bus is a bus protocol that was developed by Bosch in the 1980s. To simplify the increasing wiring of individual electronic components, sensors and actuators in the motor vehicle, the introduction of a bus system became necessary. The bus system was to have a high level of security against electromagnetic interference, be real-time capable and reliable, and above all be cost-effective for series applications. Physically, the isobus is based on the CAN bus.
The CAN bus (Controller Area Network) is a serial bus system with equal nodes. Each individual node in the network can initiate communication, i.e. send and receive independently. Unlike other protocols, CAN does not address the participants, but the message that is transmitted. The information sent is received by all nodes. Each participant can decide whether the message is important for him or not.
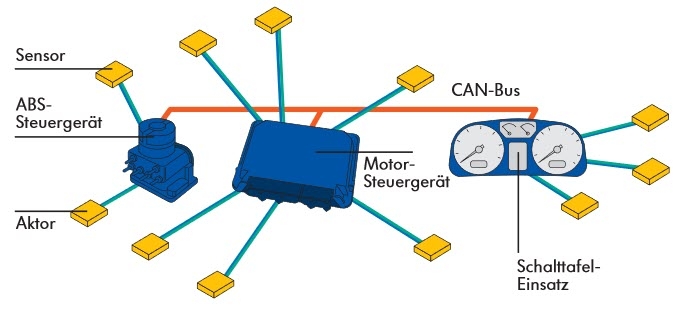
Isobus

Isobus is a standard that enables the exchange of data and information between tractors and implements thanks to a universal language and is based on a CAN bus system. Here, the individual hydraulic cylinders or electric motors are no longer controlled individually by levers or switches in the tractor, but commands are sent to the implement via a single cable. There sits a small computer, the so-called "job computer", which receives the commands and controls the necessary hydraulic valves or starts electric motors on the device.
Isobus in short form:
- Communication standard between all system components (tractor, device, universal terminal) (ISO standard: 11783)
- Foundation of the Competence Center Isobus (CCI) in 2009 by 6 manufacturers with the aim of jointly developing Isobus solutions
- Development of interfaces for data exchange and connection of devices
- Software applications can be uploaded to the CCI terminals with customer-specific settings
- Availability of apps for section control, documentation, quantity adjustment
Use of Isobus
- optimal setting of the implement: Display of setting values with the possibility of changing, saving, and recalling them.
- easy handling and operation: between the tractor and the implement there is no longer an infinite number of cables and hydraulic hoses to be coupled, but only a pressure line and a pressureless return line, as well as a BUS cable through which the power and commands are sent to the implement.
- various functions on the implement can be operated from the tractor seat while driving
- If the tractor has a BUS terminal, there is also no need for individual control boxes for each implement. The terminal automatically recognizes the connected device.
The most important Isobus modules

AEF ISOBUS database
With just a few mouse clicks, users can check which functionalities a particular product supports. It is also possible to see which functionalities are supported by a particular combination of tractor, terminal and attachment.
TIM - Tractor Implement Management - The device controls the tractor
TIM (in German: Traktor-Geräte-Management oder Gerät-steuert-Traktor) is a cross-product and cross-manufacturer ISOBUS solution in the agricultural machinery industry in which the implement can control certain tractor functions. The key to this new technology is to take advantage of the overall system, consisting, for example, of tractor and implement

© AGCO
Whereas with other solutions, only the tractor controls the attachment, with TIM, experts talk about bidirectional communication, i.e. an exchange in which data is transmitted in both directions. This means that with the help of TIM, an attachment can automatically control certain functions of the tractor - for example, the loader wagon takes over control of the tractor speed. It determines the optimum working speed for picking up the material, depending on various parameters such as swath volume.
RFID

A system for the wireless transmission of information by means of tiny so-called transponders or tags. In their simplest form, they are used only for the secure identification of living beings and products.
Sensor technology
Radio Frequency Identification - identification via electromagnetic waves. For the application of the technology a system of transmitter and receiver is necessary, which consists of a transponder and a reader. The reader generates a high-frequency electromagnetic alternating field to which the RFID transponder (RFID tag) is exposed. The high-frequency energy absorbed by it via the antenna serves as a power supply for its chip during the communication process. The microchip in the RFID tag, activated in this way, decodes the commands sent by the reader. The RFID tag encodes and modulates the response into the radiated electromagnetic field by field weakening. Thus, the tag transmits its serial number (UID) or other information requested by the reader. The tag itself therefore does not generate a field, but influences the electromagnetic transmission field of the reader.
UHF RFID/ RFID UHF (ultra-high frequency) is the latest generation and has a higher data transfer speed than LF or HF.
The reading range is much higher and you can detect several hundred transponders in parallel. This makes it possible to record the movement pattern of all animals in a group and draw conclusions about lameness or fever, for example. It would also be possible to determine the exact location of the animal because the transmitter sends its position to the receiver every second. For example, this would enable the farmer to find pigs in group housing more quickly.
Applications
Animal identification e.g. cows at the concentrate feeder, sows at boar pens, whereabouts of animals in the barn, documentation of temperature in a cold chain from the producer to the processor. Further applications. Wireless measurement of blood pressure by nano RFID chips in the bloodstream of animals. pH-value and temperature measurement in the rumen of dairy cows.
Serial interface RS-232

The serial interface is a colloquial term for an interface for data transmission between two devices, where individual bits are transmitted one after the other in time (serial data transmission).
RS-232 (Recommended Standard 232) is a standard for a serial interface that was developed in the early 1960s by the US standardization body Electronic Industries Association (EIA) and was frequently present on computers until the 2010s. This interface is also known as the COM interface and is used, among other things, to transmit position data from a satellite receiver or modem to the tractor terminal. Since the antenna is mounted outside, the connection to the computer must be established via a serial cable. To set up serial communication, a correct port number and the speed of data transmission must be specified.
Ethernet
Ethernet is a technology that subdivides software (protocols, etc.) and hardware (cables, distributors, network cards, etc.) for wired data networks. They are the basis for local data networks (LANs) and are therefore also referred to as LAN technology. (according to Wikipedia).
It enables the exchange of data between devices (computers, printers and the like) connected in a local area network (LAN). Transmission rates of < 100 megabits/s (Fast Ethernet) > 1 gigabit/s (Gigabit Ethernet) are currently specified. In its original form, the LAN extends only over one building. The Ethernet protocols include specifications for cable types and connectors as well as for transmission forms (signals on the physical layer, packet formats). Ethernet largely complies with IEEE standard 802.3 (Institute of Electrical and Electronics Engineers -> a collection of standards for cable-based networks).
RJ-45

linksys.com
An RJ45 is a system cable or connector in Ethernet and can support all transmission speeds of Ethernet commonly used today according to IEEE 802.3. These are among others Fast Ethernet 100 Mbit/s, Gigabit Ethernet and for future applications also 10 Gbit/s Ethernet.
WiFi/ WLAN
Wi-Fi
WiFi is a term of art invented for marketing purposes, formed by analogy with Hi-Fi. Whether it is an abbreviation like the latter is in doubt; the Wi certainly stands for "wireless". Wi-Fi is often used as a synonym for WLAN. Strictly speaking, however, WLAN and Wi-Fi are not the same thing: WLAN refers to the wireless network, while Wi-Fi refers to certification by the Wi-Fi Alliance (Wi-Fi-certified products are thus 802.11-compliant). (Wikipedia)
WLAN
WLAN is an abbreviation for Wireless Local Area Network. WLAN is used to dial into the Internet via a wireless connection with a computer or mobile device. This connection is made via the so-called WLAN router. This increases mobility, since access to the Internet or to one's own data pool is available anywhere in the building.
Hotspot
Hotspot is a wireless connection to the Internet. Hotspots are therefore places where you can access the Internet with a mobile device. You can also quickly set up a hotspot yourself with your cell phone using the corresponding function (e.g. personal hotspot). Thus, other devices can connect to the Internet of one's own cell phone. The hotspot should be provided with a password.
Satellites
Satellite communication enables data to be sent and received anytime and anywhere - even on board ships, in airplanes and in remote regions with no or poor Internet connections.
Position data
Satellites orbit the earth on circular paths at an altitude of 20,200 km. Seen from Earth, the satellites are constantly in motion. Each satellite constantly broadcasts its current position data on its orbit and its exact atomic clock time. The data signal with a data rate of 50 bit/s and a frame period of 30 s is transmitted on two frequencies: L1 and L2 frequency; by transmitting on two frequencies, ionospheric effects that lead to an increase in transit time can be factored out, which increases accuracy.
Earth Observation & Meteorology
Satellite-based earth observation provides information on the condition of arable soils and crops. Repeated images taken over the course of the year provide up-to-date insights into the inner workings of plants - how high their chlorophyll or water content is, how well they are supplied with nutrients, and what yields can be expected. A weather satellite is an Earth observation satellite used to observe meteorological processes, i.e. physical and chemical processes in the Earth's atmosphere. Most weather satellites measure electromagnetic radiation from the Earth's surface and atmosphere. There are active instruments, which emit radar or laser beams and measure the reflected signal, and passive instruments, which detect and evaluate the given radiation.
Telecommunications & Internet
Internet via satellite is satellite-based broadband Internet access. Geostationary satellites are frequently used for this purpose. However, there are also satellite constellations in low and medium earth orbit (LEO and MEO) that can be used for Internet access. With OneWeb and Starlink, two new large constellations of several hundred and thousand satellites respectively have been under construction since 2019.


